2964. Magnetic Cushions
The City of
the Future is built up with skyscrapers. To move between them and transport
parking some of skyscrapers triples are connected with triangular cushions made
from unipolar magnets. Each cushion connects exactly 3 skyscrapers and a top
view on it is a triangle with vertices in skyscrapers. This allows moving
freely between the skyscrapers. The pillows can be constructed at different
levels, so one skyscraper can be connected with different couples using
different pillows, so two skyscrapers can be connected with multiple pillows
(either with different third skyscraper or with the same). For example, there
may be two cushions at different levels between skyscrapers 1, 2 and 3, and
moreover, a magnetic cushion between 1, 2 and 5.
The system
of magnetic pillows is organized so that you can use them to get from one
skyscraper to any other in this city (from one pillow to another you can move
inside a skyscraper), but maintaining each of them requires a lot of energy.
Write a program that finds
which magnetic pillows can not be removed from the city structure, because removal of even just one of them leads to
the fact that there exist skyscrapers from which now you can not get to some
other skyscrapers, and people will become very sad.
Input. The first line contains two
integers n and m (3 ≤ n ≤ 105,
1 ≤ m ≤ 105) –
the number of skyscrapers in the city and the number of magnetic pillows
correspondingly. In each of the next m
lines three integers are given – the numbers of skyscrapers, connected with a
cushion. The skyscrapers are numbered with integers from 1 to n. It is guaranteed that the given
magnetic cushions allow you to move from any skyscraper to any other.
Output. Print the number of magnetic
pillows, which to turn off is impossible without breaking the connectivity in
the city. If this number is non-zero, print in the next line their numbers. The
numbers should correspond to the order in which the cushions are listed in the
input. The numbering starts from one.
|
Sample input 1 |
Sample output 1 |
|
5 4 1 2 3 2 4 3 1 2 4 3 5 1 |
1 4 |
|
|
|
|
Sample input 2 |
Sample output 2 |
|
3 2 1 2 3 3 2 1 |
0 |
|
|
|
|
Sample input 3 |
Sample output 3 |
|
3 1 1 2 3 |
1 1 |
SOLUTION
graphs – articulation points
Algorithm analysis
For the magnetic
cushion, we introduce an additional vertex, connecting it to each vertex that
is connected by this cushion. Let’s number the new vertices from n + 1 to n + m. The constructed graph will contain n + m vertices. Next,
find all articulation points with numbers greater than n. If vertex i (i > n) is an
articulation point, then this means that switching off magnetic cushion number i – n is impossible
without reporting a violation in the city.
Example
In the first sample there are 5
skyscrapers and 4 magnetic cushions, placed as shown below.
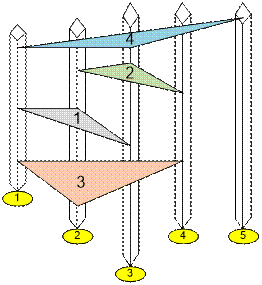
If pillow number 4 is removed,
skyscraper number 5 will
be cut off from the rest of the buildings.
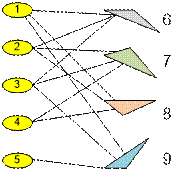
Let’s build a graph
of 5 + 4 = 9 vertices as described in the analysis of the algorithm. The
resulting graph has one articulation point 9, the number of which is greater
than 5. Therefore, the pillow number 9 – 5 = 4 cannot be
removed without breaking the connectivity in the city.
Algorithm realization
Declare the arrays. Store the graph
as an adjacency list in the array graph.
vector<int> graph[MAX];
int used[MAX], d[MAX], up[MAX], ArtPoints[MAX];
Function dfs runs the depth first search, where the arrays d and up are built and the articulation points are found. ArtPoints[v] is set to 1 if the vertex v is the articulation point. Otherwise ArtPoints[v] is set to 0.
void dfs (int v, int p = -1)
{
used[v] = 1;
d[v] = up[v] = time++;
int children =
0;
for (int i = 0; i < graph[v].size(); i++)
{
int to =
graph[v][i];
if (to ==
p) continue;
if
(used[to])
up[v] = min (up[v], d[to]);
else
{
dfs (to, v);
up[v] = min (up[v], up[to]);
if
((up[to] >= d[v]) && (p != -1)) ArtPoints[v] = 1;
children++;
}
}
if ((p == -1)
&& (children > 1)) ArtPoints[v] = 1;
}
The main part of
the program. Read the
input data. Build the graph.
scanf("%d %d",&n,&m);
Vertices = n + m;
memset(used,0,sizeof(used));
memset(d,0,sizeof(d));
memset(up,0,sizeof(up));
memset(ArtPoints,0,sizeof(ArtPoints));
for(i = 1; i <= m; i++)
{
scanf("%d %d
%d",&v1,&v2,&v3);
graph[n+i].push_back(v1);
graph[v1].push_back(n+i);
graph[n+i].push_back(v2);
graph[v2].push_back(n+i);
graph[n+i].push_back(v3);
graph[v3].push_back(n+i);
}
Run
the depth first search on the graph, find all articulation points.
time = 1;
for(i = 1; i <= Vertices; i++)
if (!used[i])
dfs(i);
Count the
number of articulation points cntArtPoints.
int cntArtPoints = 0;
for(i = n + 1; i <= Vertices; i++)
if
(ArtPoints[i]) cntArtPoints++;
Print
the number of articulation points.
printf("%d\n",cntArtPoints);
Print the
numbers of magnetic pillows, the
removal of which is impossible without breaking the connectivity in the
city.
if (cntArtPoints)
{
for (i = n + 1; i <= Vertices; i++)
if (ArtPoints[i]) printf("%d
", i - n);
printf("\n");
}
Java realization
import java.util.*;
public class Main
{
static ArrayList<Integer>[] g;
static int used[], up[], d[], ArtPoints[];
static int time;
static void dfs (int v, int p)
{
used[v] = 1;
d[v] = up[v] = time++;
int children = 0;
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (to == p) continue;
if (used[to] == 1)
up[v] = Math.min(up[v], d[to]);
else
{
dfs (to, v);
up[v] = Math.min(up[v], up[to]);
if ((up[to] >= d[v]) && (p != -1)) ArtPoints[v] = 1;
children++;
}
}
if ((p == -1) && (children > 1)) ArtPoints[v] = 1;
}
@SuppressWarnings("unchecked")
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
g = new ArrayList[n+m+1]; // unchecked
used = new int[n+m+1];
up = new int[n+m+1];
d = new int[n+m+1];
ArtPoints = new int[n+m+1];
for (int i = 0; i <= n + m; i++)
g[i] = new ArrayList<Integer>();
for (int i = 1; i <= m; i++)
{
int v1 = con.nextInt();
int v2 = con.nextInt();
int v3 = con.nextInt();
g[n+i].add(v1); g[v1].add(n+i);
g[n+i].add(v2); g[v2].add(n+i);
g[n+i].add(v3); g[v3].add(n+i);
}
time = 1;
for(int i = 1; i <= n + m; i++)
if (used[i] == 0) dfs(i,-1);
int cntArtPoints = 0;
for(int i = n + 1; i <= n + m; i++)
if (ArtPoints[i] == 1) cntArtPoints++;
System.out.println(cntArtPoints);
if (cntArtPoints > 0)
{
for (int i = n + 1; i <= n + m; i++)
if (ArtPoints[i] == 1) System.out.print(i - n + "
");
System.out.println();
}
con.close();
}
}